Network Associations
Here's a very simple project that answers a fundamental question for anomaly detection. How many unique hosts does my little workgroup network talk to, and are they persistent, transient? A simple graph can provide us with some interesting answers here.
MySQL Data Store
Argus data collected from the exterior border of QoSient world headquarters (WHQ), is processed to generate a persistent MySQL database table of all the IP addresses that QoSient has ever seen. This table is constantly available and is upto date within 5 seconds of realtime.
rasqlinsert -S amon -w mysql://root@localhost/ratest/IPHost -M rmon cache -m srcid smac saddr - ip
rasqlinsert() attaches to amon, which is my radium() based collection node that has all the flow data from QoSient WHQ. rasqlinsert() processes the data to track just single unique IP addresses, using the probe identifier "srcid", the ethernet address "smac", and IP address "saddr" as the aggregation key. This writes data into the local MySQL database table "IPHost", in the "ratest" database.
As data arrives, rasqlinsert() aggreates records that share the same "srcid smac saddr" key, resulting in an entry for every IP address that every probe observes, with the metrics aggregated. So we'll get things like start time (the first observed occurence of the IP address), duration (total time seen since the beginning). This schema is great for our question, how many unique IP addresses are there, and how long have I been talking to them.
Graph Data Generation
A graph that can answer our question is a frequency distribution of the durations of the IP addresses in our IPHost table. This is very easy to generate, using the programs rasql() and rahisto(). So I've been running the rasqlinsert() for a week, so I'll just graph the whole table. A week is a good initial time period for the study, and so lets generate a log frequency distribution of the durations of each unique IP address, with 50 bins, ranging from 0.0001 to 1,000,000 seconds (1 week is about 604,800 seconds).
For this graph, we want to see just the number of IP addresses that fall into a particular bin. To get that simple number, we need to remove the AGR DSR that each flow record contains. If we don't remove the AGR DSR, we'll get the number of argus records that were merged to create the row in the MySQL database. May seem complicated, but the more you use these tools, of course, the more they may make sense. OK, the encantation below will give us the data we need for the graph.
rasql -r mysql://root@localhost/ratop/etherHost -w - | rahisto -M dsrs="-agr" -H dur 50L:0.0001-1000000 - pkts gt 1
So, we just dump the database table into rahisto(), and we process records that have more than 1 packet in them (so we count flows that actually have a duration). We'll take the output of rahisto() and use it to generate the graph below. Actual output is included at the bottom of this page.
Resulting Graph
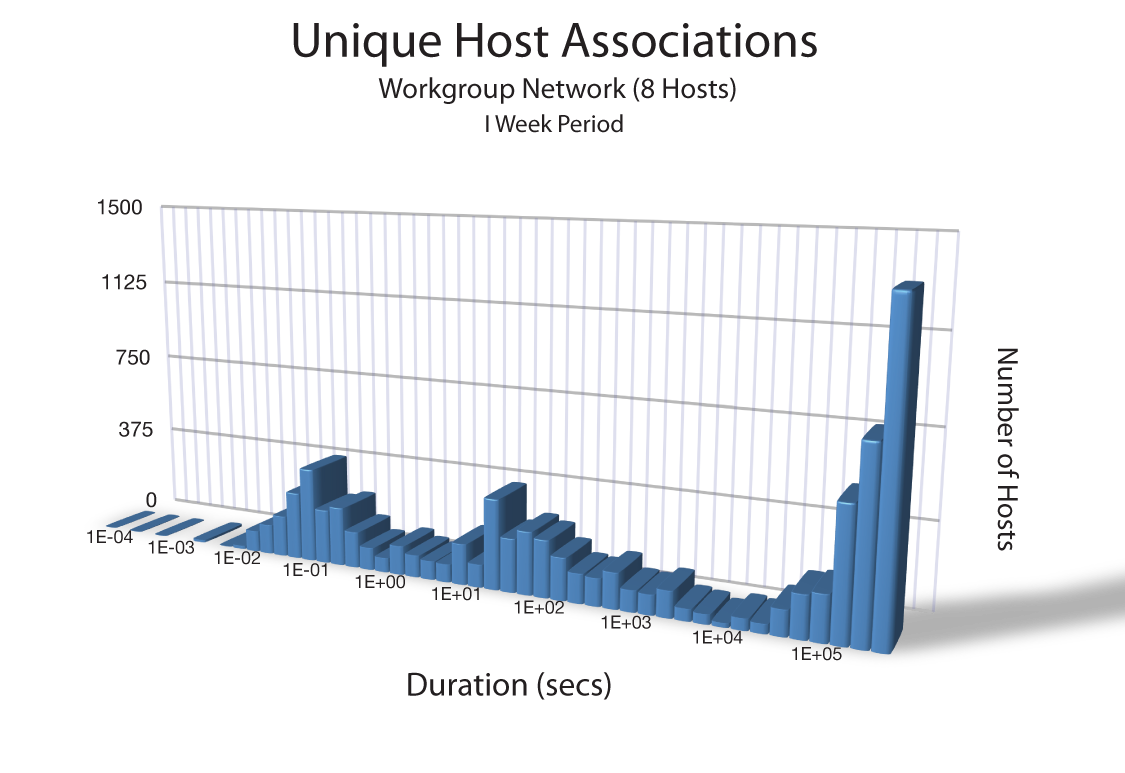
So this is a very interesting result. Basically, we've got 3 populations of IP associations from this network. We could call them
1) "infrequent" associations which only existed in the range of 0.01 - 5.0 seconds
2)
"transient" associations that lasted from 5 - 4600 seconds in this study, and then
3) "persistent" associations that lasted betwen 10,000 - 603,749 seconds (basically a week).
So during a period of 7 days, we have approximately 25% of all our associations lasting less than 5 seconds. The traffic is basically DNS transactions and web page accesses to infrequently accessed web sites. 35% of all the host associations lasted from between 5 seconds and 1 hour, and represented repeatedly accessed DNS servers and web sites, but the visitation period (if that is an acceptable term) was only an hour. So the content was possibly something interesting, but not compelling?, and then 40% of all unique address associations were repeated and persistent throughout the study period. The expectation is that as the study time increases, this 3rd population will shift to the right.
What kind of stuff is going on in this little network to have an interest in 7987 unique IP addresses in just a week? Nothing unusual at all, really. Web browsing, email, and DNS. There are Mac OS X and Linux machines, predominately, with a single virtual copy of Windows XP, which isn't running for more than 1 hour at a time (maybe a clue). Each of these machines will want to phone home for updates, and each have a lot of software, supporting cellphones, remote calendar and filesystem synchronization.
I think the surprise is not that there are so many IP addresses, but that there are so many persistent IP addresses (> 3100) supporting a small number of machines.
OK, graph generated using Apple's Numbers '09 program, data generated by argus(), rasqlinsert(), rasql() and rahisto().
Here is the data output by rahisto(). Using the "-c ','" option, I generated a data.csv file that could be read in by Numbers '09, Excel, or gnuplot().
N = 7987 mean = 136364.031250 stddev = 198276.234375 max = 603749.375000 min = 0.000125
median = 303.719055 95% = 572877.875000
mode = 478271.750000
Class Interval Freq Rel.Freq Cum.Freq
1 1.000000e-04 1 0.0125% 0.0125%
2 1.584893e-04 0 0.0000% 0.0125%
3 2.511886e-04 2 0.0250% 0.0376%
4 3.981072e-04 0 0.0000% 0.0376%
5 6.309573e-04 2 0.0250% 0.0626%
6 1.000000e-03 0 0.0000% 0.0626%
7 1.584893e-03 0 0.0000% 0.0626%
8 2.511886e-03 11 0.1377% 0.2003%
9 3.981072e-03 0 0.0000% 0.2003%
10 6.309573e-03 2 0.0250% 0.2254%
11 1.000000e-02 14 0.1753% 0.4007%
12 1.584893e-02 93 1.1644% 1.5650%
13 2.511886e-02 131 1.6402% 3.2052%
14 3.981072e-02 181 2.2662% 5.4714%
15 6.309573e-02 296 3.7060% 9.1774%
16 1.000000e-01 412 5.1584% 14.3358%
17 1.584893e-01 237 2.9673% 17.3031%
18 2.511886e-01 257 3.2177% 20.5208%
19 3.981072e-01 158 1.9782% 22.4991%
20 6.309573e-01 98 1.2270% 23.7261%
21 1.000000e+00 63 0.7888% 24.5148%
22 1.584893e+00 126 1.5776% 26.0924%
23 2.511886e+00 96 1.2020% 27.2944%
24 3.981072e+00 81 1.0141% 28.3085%
25 6.309573e+00 78 0.9766% 29.2851%
26 1.000000e+01 177 2.2161% 31.5012%
27 1.584893e+01 99 1.2395% 32.7407%
28 2.511886e+01 389 4.8704% 37.6111%
29 3.981072e+01 231 2.8922% 40.5033%
30 6.309573e+01 271 3.3930% 43.8963%
31 1.000000e+02 246 3.0800% 46.9763%
32 1.584893e+02 183 2.2912% 49.2676%
33 2.511886e+02 127 1.5901% 50.8576%
34 3.981072e+02 119 1.4899% 52.3476%
35 6.309573e+02 154 1.9281% 54.2757%
36 1.000000e+03 92 1.1519% 55.4276%
37 1.584893e+03 86 1.0767% 56.5043%
38 2.511886e+03 114 1.4273% 57.9316%
39 3.981072e+03 52 0.6511% 58.5827%
40 6.309573e+03 42 0.5259% 59.1085%
41 1.000000e+04 19 0.2379% 59.3464%
42 1.584893e+04 50 0.6260% 59.9724%
43 2.511886e+04 41 0.5133% 60.4858%
44 3.981072e+04 110 1.3772% 61.8630%
45 6.309573e+04 181 2.2662% 64.1292%
46 1.000000e+05 194 2.4289% 66.5581%
47 1.584893e+05 551 6.8987% 73.4569%
48 2.511886e+05 789 9.8786% 83.3354%
49 3.981072e+05 1331 16.6646% 100.0000%
50 6.309573e+05 0 0.0000% 100.0000%
